Playing around with the great pyramid.
Length of base + height = 440 + 280 = 720 royal cubits.
720/360 = 2 (save this for later)
If we convert to digits by multiplying by 28 (because 28 digits in royal cubit), we get
720 x 28 = 20160
If we divide by 360, we get
20160/360 = 56, which is the number of digits in 2 cubits (see saved value of 2)
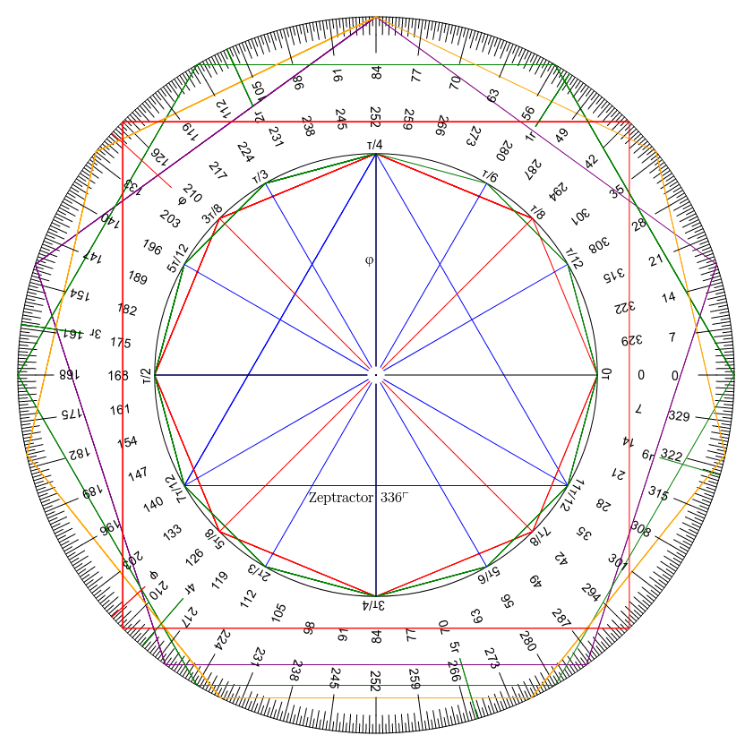
As you may know, I’m developing a theory that whoever came up with the cubit system also divided the circle into 336 Zeps. So if we divide by 336 instead….
20160 / 336 = 60
Which is um, all sorts of things, and maybe a hat-tip (or the finger) to the Sumerians and their sexagesimal system.
But what the 60 also equates to, is if you had a wheel of radius 1 metre, then 60 rolls of the wheel would equal the sum of the side and the height.
If your wheel had a diameter of 1 metre (like a chariot), then it would be 120 turns of the wheel. Exactly.