In Part 1 we dealt with numbers and ratios that were not unknown in the ancient world, even if we still think it was the Greeks that invented π and φ and the whole Pythagoras theorem etc.

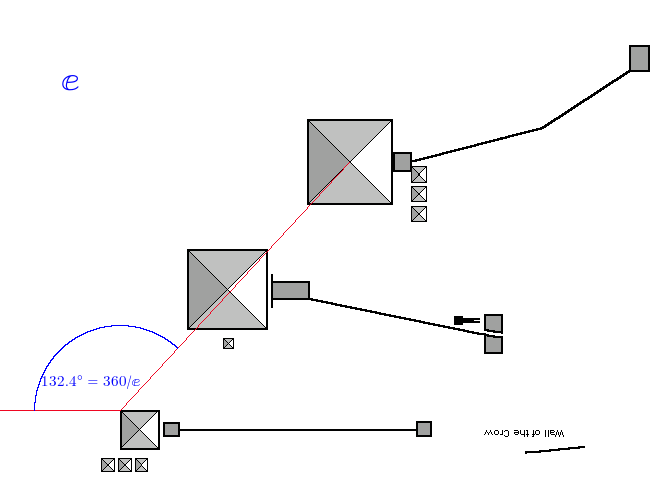
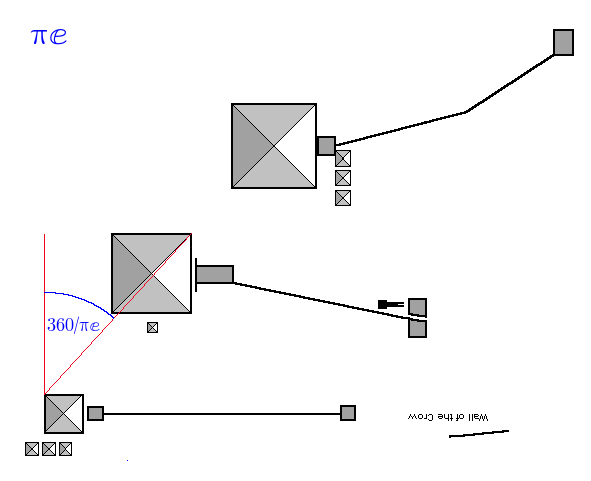
Now we introduce ℯ (2.71828…), the base of the natural logarithm, which is defined as the limit of (1 + 1/n)ⁿ  as n approaches infinity. There is no evidence that the Egyptians knew of this number, but here it is:

The angle is 132.340, we want 132.437, out by 0.096 degrees, accuracy is 99.927%

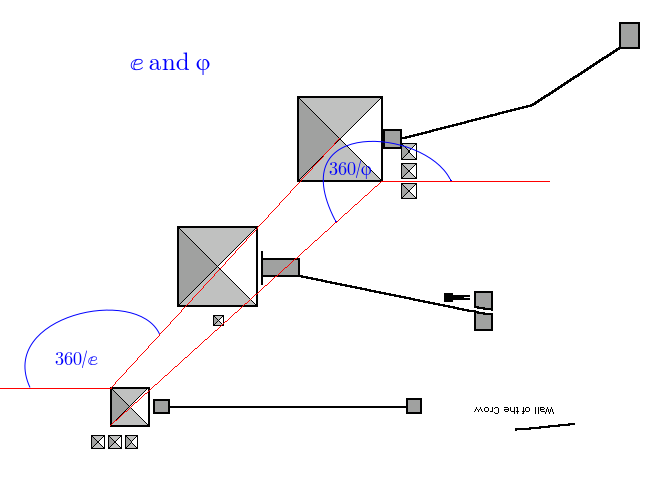
ⅇ and φ are nicely balanced:

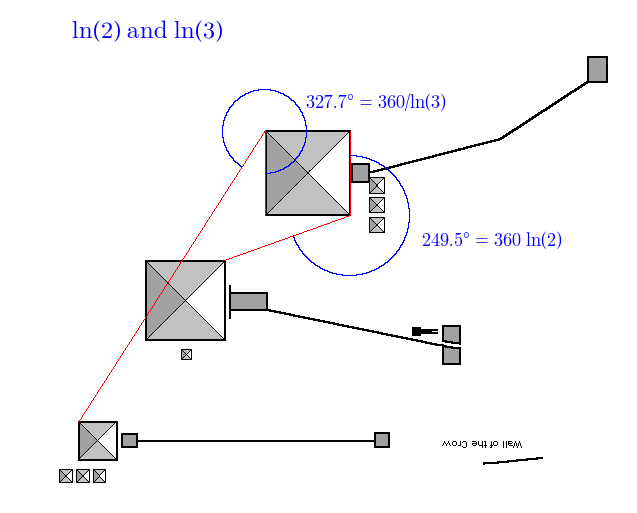
And now for something much more controversial … logarithms in base ⅇ. We have no indication that the Egyptians knew of them, but we can demonstrate both ln(2) and ln(3) here, once more based off of the great pyramid and linking all three:

Name	Ratio	Point 1	Point 2	Calculated	Desired	AbsDiff	Percentage	Error %
ⅇ	360/ⅇ	P3 TL	P1 C	132.340	132.436	0.0962	99.927	0.073
ln2	360(ln2)	P1 BR	P2 TR	248.957	249.533	0.576	99.769	0.231
ln3	360/ln3	P1 TL	P3 TL	327.518	327.686	0.168	99.949	0.051

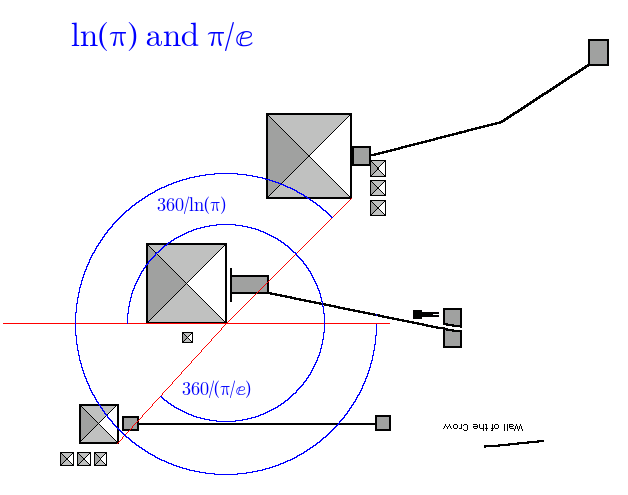
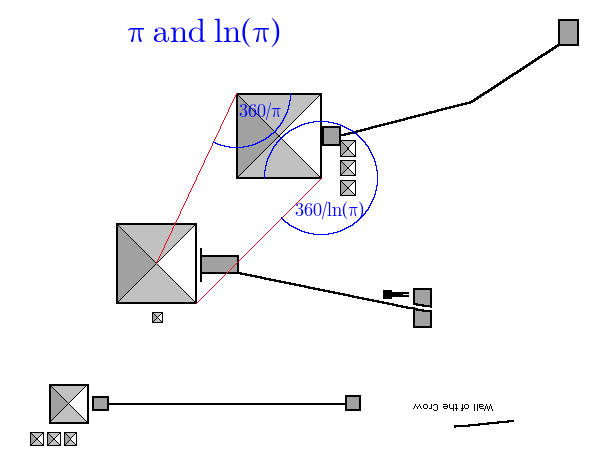
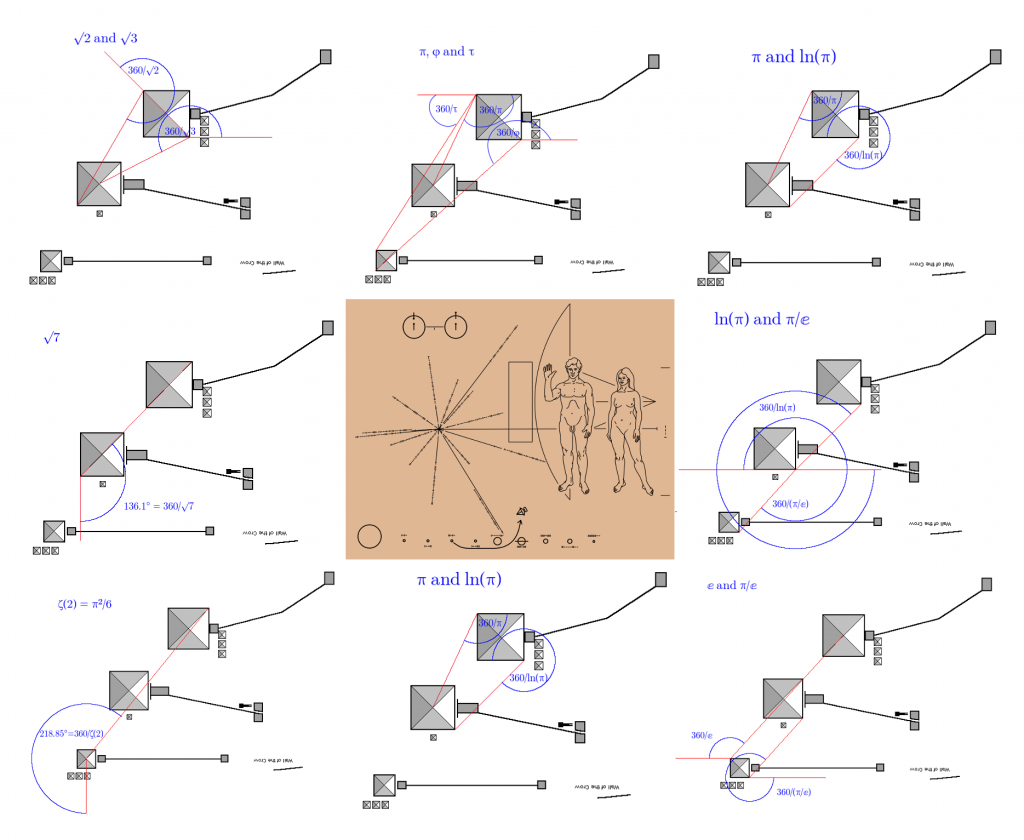
Here’s ln(π):

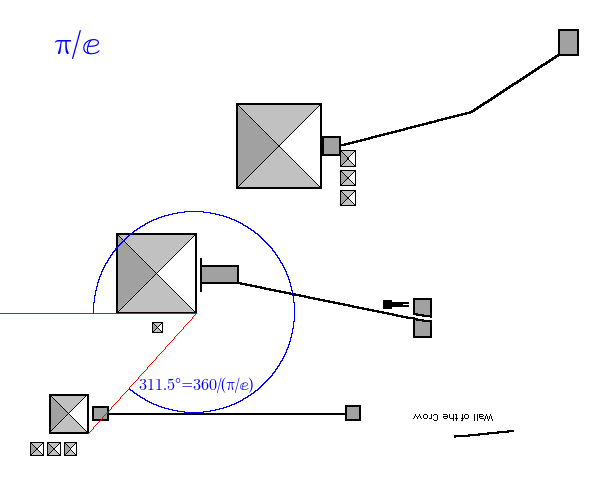
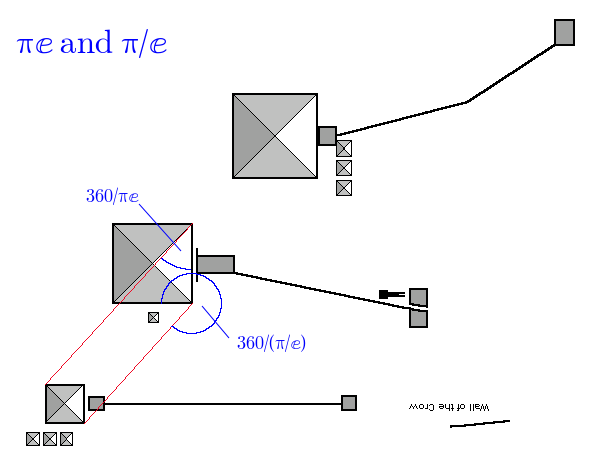
and π/ⅇ:

And πⅇ:

The accuracy is quite worrying.

Name	Ratio	Point 1	Point 2	Calculated	Desired	AbsDiff	Percentage	Error %
ln(π)	360/ln(π)	P2 BR	P1 BR	314.550	314.485	0.066	100.021	0.021
π/ⅇ	360/(π/ⅇ)	P2 BR	P3 BR	311.672	311.492	0.180	100.058	0.058
πⅇ	360/πⅇ	P3 TL	P2 TR	42.213	42.156	0.057	100.135	0.135

Which leads us to this beautifully symmetrical arrangement of ln(π) and π/ⅇ

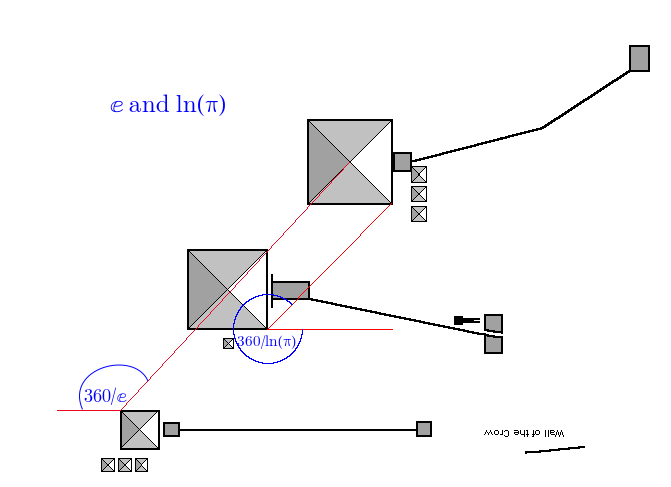
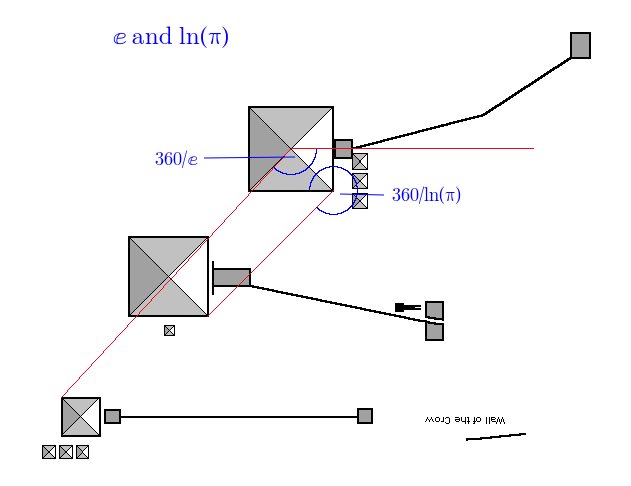
ⅇ and ln(π) are also nicely balanced:

Or this way around:

Or π and  ln(π):

And ⅇ and π/ⅇ :

And not forgetting πⅇ and π/ⅇ :

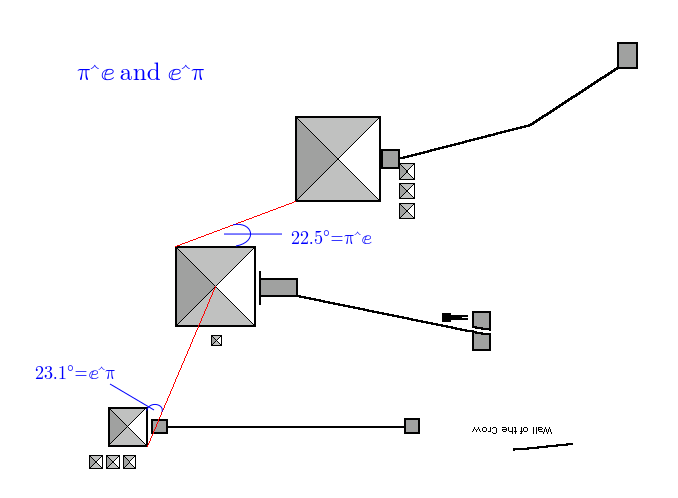
Then we have π^ⅇ and ⅇ^π… (not really happy with π^ⅇ but will have to do for now):

For π^ⅇ, the angle is 21.940, we want 22.459, out by 0.519 degrees, accuracy is 97.690%

For ⅇ^π, the angle is 23.076, we want 23.141,  out by 0.065 degrees, accuracy is 99.718%

The Omega constant Ω also belongs in this section. The Omega constant is the number for which Ωⅇ^Ω = 1, which is Ω = 0.567143290…. :

The angle is 204.060, we want 204.172, out by 0.111 degrees, accuracy is 99.945%

And lastly, we have √τⅇ = √2πⅇ  (4.1327313541…), which like the Omega constant above, I’m not entirely sure where the practical use is, but it’s on Wikipedia’s list of mathematical constants so I guess it does have a use somewhere.

The angle is 87.003, we want 87.109, out by 0.107 degrees, accuracy is 99.878%

In summary, for this page:

Name	Ratio	Point 1	Point 2	Calculated	Desired	AbsDiff °
ⅇ	360/ⅇ	P3 TL	P1 C	132.340	132.437	0.096
ln2	360(ln2)	P2 TR	P1 BR	248.957	249.533	0.576
ln3	360/ln3	P3 TL	P1 TL	327.518	327.686	0.168
ln pi	360/(ln pi)	P2 BR	P1 BR	314.550	314.485	0.066
π/ⅇ	360/(π/ⅇ)	P3 BR	P2 BR	311.672	311.492	0.180
πⅇ	360/πⅇ	P3 TL	P2 TR	42.213	42.156	0.057
pi^e	pi^e	P2 TL	P1 BL	21.940	22.459	0.519
e^pi	e^pi	P2 C	P3 BR	23.076	23.141	0.065
Omega	360Ω	P3 BR	P1 TL	204.060	204.172	0.111
√τⅇ	360/√τⅇ	P3 C 45°	P1 BR	87.003	87.109	0.107
Average						0.194

So if we can quote Robert Bauval again, how many pigeons do we need before we decide it’s not co-incidence?

The best explanation I can think of for these curious alignments (apart from the builders simply showing off) is to send a message down through the ages… Yes, we are intelligent, and yes, we can do mathematics….

Continues in Part 3