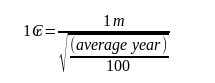[Note: I’m not entirely convinced that my “average year” calculations are correct. I was looking for a way to get 364.75 and since it is tantalizingly close to 365.25 I was looking for a way to get there from that. It may be better to just use 365.25 – 0.5 … now need a Reason Why.]
I was playing around with the calculator and stumbled across this curious sum.
Let’s start with how long a year is. As you should know, it’s 365.25 days for a solar year. If however, we measure against the background stars, it’s about 364.25 days.
From Wikipedia: “Both the stellar day and the sidereal day are shorter than the mean solar day by about 3 minutes 56 seconds. ”
If we take those 3 minutes 56 seconds == 236 seconds, and work out the difference over a year (x 365), we get 86140 seconds, which is 23.927777 hours, effectively one day.
So if we take the average of a solar year and stellar year, we get (365.25 + 364.25)/2 which is 364.75 days, or more precisely, 364.7436921 days.
Now we do this sum.
I can’t justify the steps (yet, and why it’s a “curious alignment”), but just bear with me:
- take the square root. √364.7436921 = 19.09826411
- divide by 10: 1.909826411
- take the inverse: 1/1.909826411 = 0.5236077971
- Compare to royal cubit in metres, π/6 : 0.5235987756
- Correct to 4 decimal places: 0.5236
- Converting the original 0.5236032695 back to metres (x 6/π) gives 1.00001723 metres.
Now need to figure out WHY those steps, and what it all means …..
I actually stumbled across this by doing some of the steps in reverse, i.e. starting with the cubit, taking the inverse, and squaring the result, and noticed the answer came out at 3.647562611. Hence the “divide by 10” step above to scale the answer, else you end up with decimal place in inconvenient spot.
So you could do this without the “divide by 10” step by working with “1 percent of average year”, i.e. 3.6475. Which in words, becomes “One cubit is one over the square root of one percent of the average year in days”, or to put into a formula, using the now-defunct Brazilian Cruzeiro ₢ sign for the Royal Cubit:
Cubit formula from length of year
Or if we want to scale to 1 metre….
Metre formula from length of year
[Yes I know I should maybe be talking about metres/day of some-such …]
A bit or re-arranging gives us this:
Average year length based on length of cubit in metres
I did in fact consider that perhaps the people who came up with the cubit had a year that was dramatically different to ours, but the Earth is slowing down by a few milliseconds per century, so it will take over a million years to slow down by half a day. So don’t think that line of thought will lead to better explanation.
Here’s a comparison table showing the various ways to get the cubit, in terms of a metre.
| Method | Value | Difference from π/6 | Abs difference |
|---|---|---|---|
| π/6 | 0.52359877559830 | 0.00000000000000 | 0.00000000000000 |
| φ²/5 | 0.52360679774998 | 0.00000802215168 | 0.00000802215168 |
| Ave Year | 0.52360779708785 | 0.00000902148956 | 0.00000902148956 |
| π – φ² | 0.52355866483991 | -0.00004011075839 | 0.00004011075839 |
As you can see, the Average Year method (above) is almost as good as φ²/5, and 4 times better than π-φ² squared..
Now I really need to figure out how they got the length of a second …
Note: see also Another cubit approximation.
Changelog:
2018-11-05: Redid the formulas to use length on right side, added formula for average year.
2018-11-06: Added cubit comparison table. Redid sums using more accurate values.
2018-11-06: Fixed typos φ²/6 => φ²/5