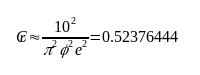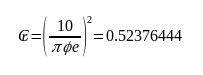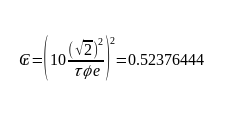After fiddling around a bit, eventually found another way of getting an approximation for the royal cubit. I say approximation because, compared to the other methods, it’s only accurate to about 3 decimal places.
The formula looks like this:
₢ == 10²/φ²π²ⅇ²
or
(10/φπⅇ)² cubit approximation
What I like about it is how it uses what are arguably the most famous numbers of all time in all of mathematics (yes, √2, you’ve just been demoted) and wraps them all nicely to produce a reasonable figure for the royal cubit.
Not quite as elegant as Euler’s famous formula, but still interesting.
By way of comparison, here’s the others:
| Method | Value | Difference from π/6 | Abs difference |
|---|---|---|---|
| π/6 | 0.52359877559830 | 0.00000000000000 | 0.00000000000000 |
| φ²/5 | 0.52360679774998 | 0.00000802215168 | 0.00000802215168 |
| Ave Year | 0.52360779708785 | 0.00000902148956 | 0.00000902148956 |
| π – φ² | 0.52355866483991 | -0.00004011075839 | 0.00004011075839 |
| 10²/π²φ²ⅇ² | 0.52376444099003 | 0.00016566539172 | 0.00016566539172 |
If we really want to keep root 2 happy, we could rewrite it like this, and cheat a bit.
Cubit with tau, phi, e and root 2
Where tau τ is equal to 2 π.