Changelog is at end of part 3.
The Giza plateau is one of the most studied places on Earth, while curiously some parts remain off-limits and unexplored. Various people have studied both the pyramids themselves, and the layout of the site, in great detail, which led to various different ideas about the site plan, which are summarised/detailed here:
1. The Orion alignment: https://en.wikipedia.org/wiki/Orion_correlation_theory
2. The Cygnus alignment: http://www.andrewcollins.com/page/articles/Cygnus_Orion_Giza.htm
3. A possible method of how it was planned: http://members.home.nl/peregrine/The%20Geometry%20of%20Giza.html
4. Another way of drawing the site: http://www.vejprty.com/gizaplan.htm
5. Another analysis: http://home.hiwaay.net/~jalison/Art3.html
6. Online book with analysis: https://www.greatpyramidexplanation.com/en/index.html
7. Edward Nightingale’s analysis: https://grahamhancock.com/nightingalee1/
8. Golden ratios on the site plan: https://www.goldennumber.net/great-pyramid-giza-complex-golden-ratio/
9. [placeholder for another site with lots of maths, can’t find at the moment.]
I’ve done some analysis of my own, kicked off by looking for phi circles/arcs, which I learned about when I watched a documentary about the Nebra disc…
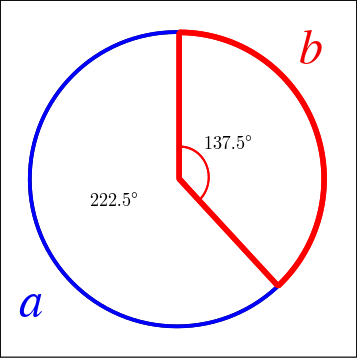
which I found fascinating. In particular (for the purposes of this post), the strange curved line at the bottom, which has been shown to be the arc of a circle after it has been divided in the golden ratio phi φ, 1.6180339887…, which for our purposes we will use 1.618 and the inverse, 0.618 as being close enough for practical purposes.
When we divide a circle in the golden ratio, we get two arcs. The red arc b corresponds to the golden arc on the disk.
When I saw that I was reminded of the “kink” in the alignment of the pyramids at Giza, and wondered if that angle could explain the kink.
No, it does not. But I’m stubborn and played around a bit, and eventually found where it was hiding. Then one thing led to another and soon I had found multiple angles related to famous irrational numbers, including π, φ, √2, √3, √5, and more…
But before we get to the Film At Eleven, I suppose a disclaimer or two is necessary:
- I originally started with paper, pencil and protractor, but that soon proved too inaccurate, so I switched to using a program with precise relative co-ordinates from Glen Dash’s precise measurements.
- I am aware of falling into the “Beautiful Mind” trap and finding patterns which happen to be there but were not put there by design.
- Working with 5 points on each pyramid, and 3 pyramids, can produce a lot of potential angles, so maybe you could find anything you were looking for. My reply to that is that the angles are relatively “simple”, i.e. generally “basic” alignments, and the angles required are based on irrational numbers … we’re not talking about 30, 45 and 60 degree angles but something much more “unusual”. And it’s curious when the fractions of the degree seem to line up….
- As Robert Bauval likes to remind us, perfection does not exist, especially when it comes to building, and even more so with something on the scale of Giza. We also have no idea how accurate their instruments were. So “a bit of slack” would not be out of line, but the results are generally pretty accurate. Also, some points were used in more than one of the following ratios, which may mean picking “best fit” for several, rather than 1 perfect and the others way off.
- I did this in The Gimp, which is pixel-based, so the diagonal lines are jagged.
- In general, I was calculating angles based on 360/x where x is some irrational. In some cases I used 360x to get a number smaller than 360. I used the differences between two points, applied the atan function to get an angle, and then adjusted it with 90/180/360/whatever to get the correct angle-baseline measurement.
Just a note on my methodology: there’s basically two ways of doing an exercise like this:
1. Measure every possible angle, then go and look for something that correlates to it. This is the sort of process that will have people measuring the diagonal of a wall in the Queen’s Chamber using Pyramid Inches, then claiming that it correlates to the average distance between Pluto and Uranus, thus “proving” that the ancient Egyptians knew about those planets and their orbits.
2. The other way is to think about what number and ratios are important mathematically, and then see if they are to be found in the layout. This is the approach I followed. I’m not claiming that the fact that there are in some cases very good matches (e.g. for φ or √7) proves anything, but the sheer number of well-known and important numbers should give one pause for thought. Achieving so many on such a limited design (three pyramids) (as well as the beautiful symmetry for some ratios) takes some doing….
3. After much thought (see changelog) I decided to retain the current methodology of measuring the angles with respect to N-S and E-W (i.e. the Cartesian plane) rather than “along the edge of the pyramid”, and adjusting for the skewness of the pyramids themselves. This is partly because most measurements can be made in both directions, so which pyramid skewness do I use to adjust with? I will leave the debate about this to others with more knowledge. The only exceptions were for those angles measured with a baseline on the diagonal of a pyramid, in which case used the actual angle rather than 45°, they are very close to 45° anyway.
Okay, with that out of the way, let’s let the pictures do the talking. The diagrams are meant to illustrate the angles involved rather than be pin-point accurate in the measurement. Exact numbers are given below each diagram.
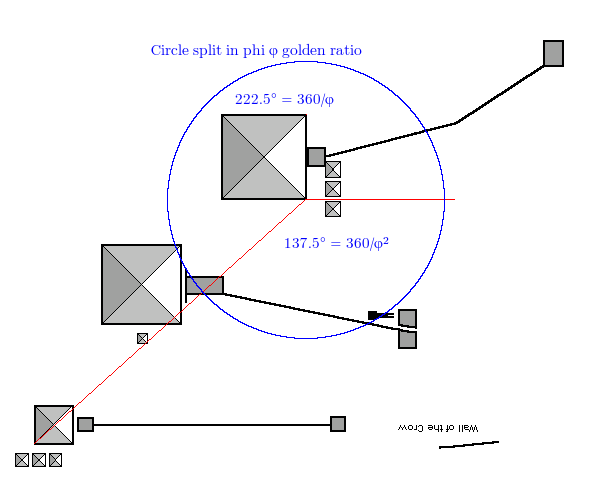
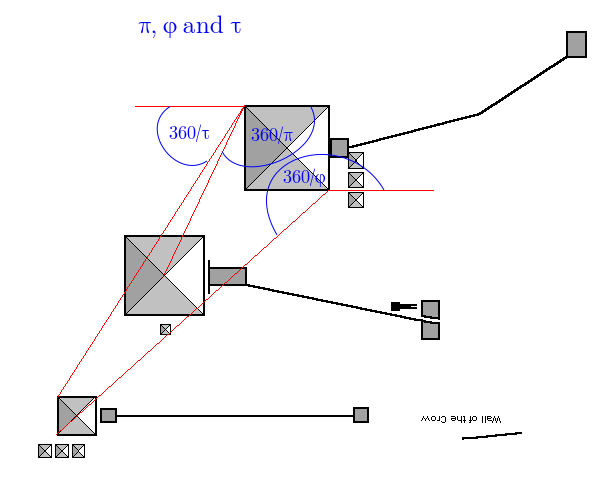
First up, is phi:
The angle is 222.4102, we want 222.4922, out by 0.082 degrees, accuracy is 99.9632%
Of course, due to the magical qualities of Phi, the above also has φ²:
The accuracy is clearly the same as for φ.
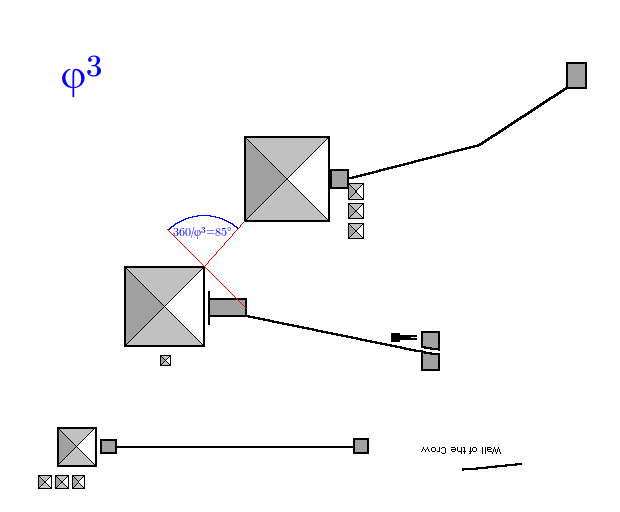
Apparently φ³ was also important to the ancient Egyptians (regret have lost link where I saw that), and here it is. The problem is that angles close to 90° are tricky to find.
The angle is 85.219, we want 84.985, out by -0.235 degrees, accuracy is 100.276%
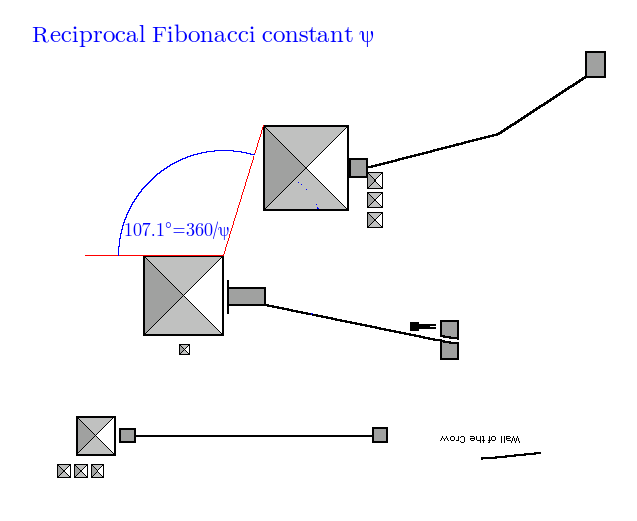
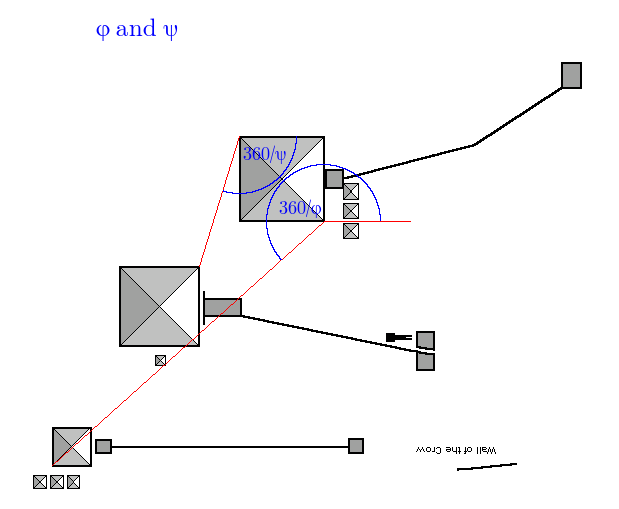
Now since phi is what successive terms of the Fibonacci series tends to, we should also look at the Reciprocal Fibonacci constant (3.359885666…. ) which is designated psi ψ:
The angle is 107.075, we want 107.147, out by 0.072 degrees, accuracy is 99.933%
And together:
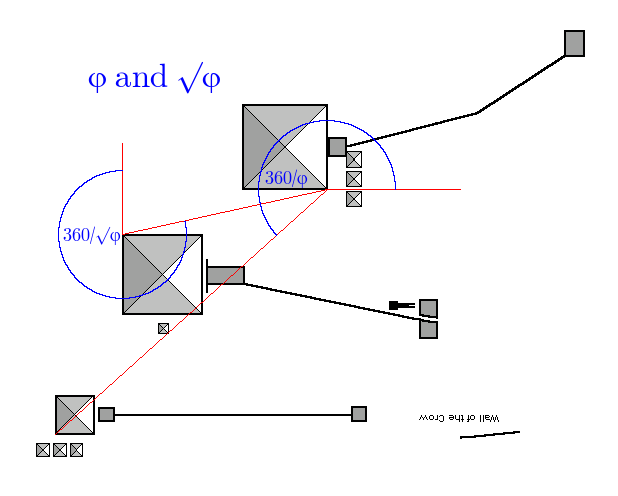
As per, for example, the analysis by Samuel Laboy, √φ was important and used in the construction of the Great Pyramid. Here it is in the plan:
The angle is 283.3104, we want 283.0145, out by -0.2959 degrees, accuracy is 100.1046%
And if we compare φ and √φ:
I could originate them both from P1 Bottom Right but the drawing will be a bit messy.
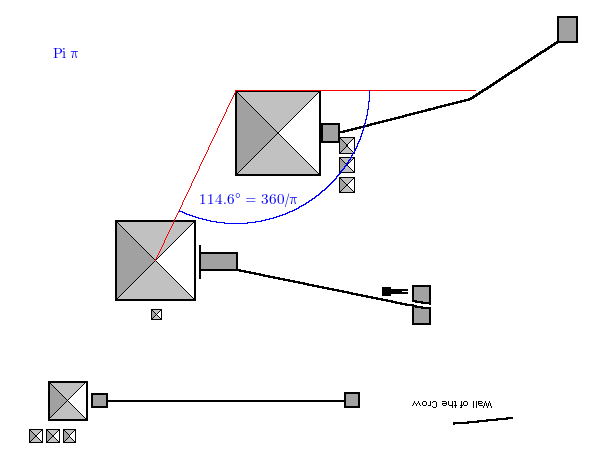
Sticking with the famous Ps, here’s pi (3.14159…):
The angle is 114.9667, we want 114.5916, out by -0.3752 degrees, accuracy is 100.3274%
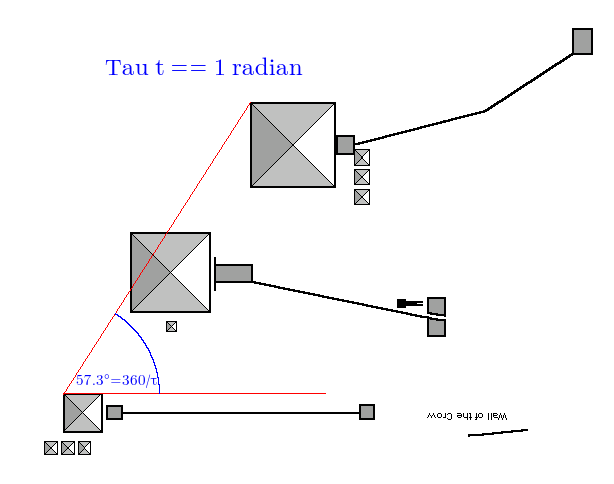
Staying with circle ratios, there is a school of thought that contends that a better “natural” circle ratio is circumference/radius, named tau τ, which is equal to 2π, (6.2831…). You can read more on The Tau Manifesto.
We can find tau here:
The angle is 57.518, want 57.296, out by -0.222 degrees, accuracy is 100.388%
And when we put all three together …
I suggest that, given it is π, φ and τ that we are talking about, and the connections between the three pyramids above, that it would be difficult to argue that this is a random fluke. So if it is not a co-incidence, then it must be by design….
| Name | Ratio | Point 1 | Point 2 | Calculated | Desired | AbsDiff |
|---|---|---|---|---|---|---|
| Phi | 360/φ | P1 BR | P3 BL | 222.410 | 222.492 | 0.082 |
| Psi | 360/ψ | P2 TR | P1 TL | 107.075 | 107.147 | 0.073 |
| Pi | 360/π | P1 TL | P2 C | 114.967 | 114.592 | 0.375 |
| Tau | 360/τ | P3 TL | P1 TL | 57.518 | 57.296 | 0.222 |
| Root(Phi) | 360/√φ | P2 TL | P1 BR | 283.310 | 283.014 | 0.296 |
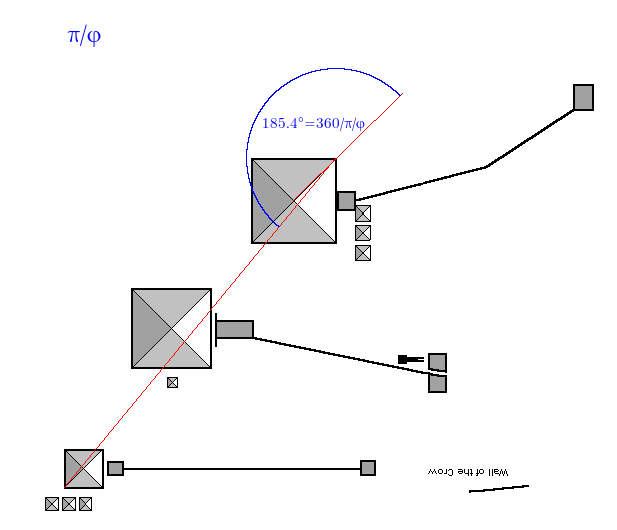
And then there’s π/φ … which provides the answer to “what is the angle joining the top right to the bottom left” ….
The angle is 185.826, want 185.413, out by -0.413 degrees, accuracy is 100.223%
Which leads to this happy construction:
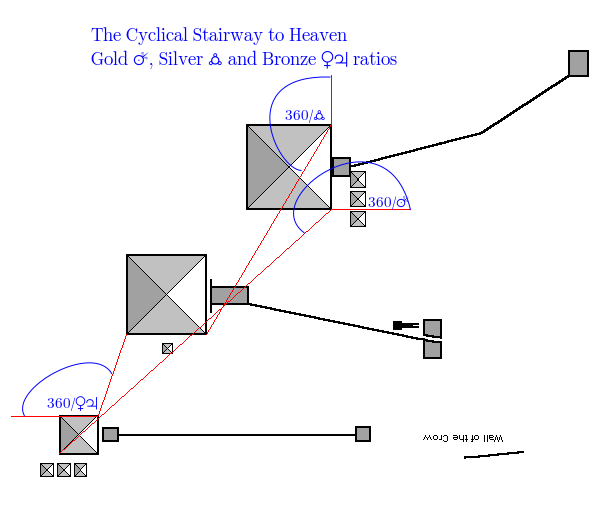
We’ve already looked at the Golden Ratio φ. The other two (Silver and Bronze) are also there:
For Silver, the angle is 149.419, we want 149.117, out by -0.302 degrees, accuracy is 100.202%
For Bronze, the angle is 109.330, we want 108.999, out by -0.331 degrees, accuracy is 100.303%
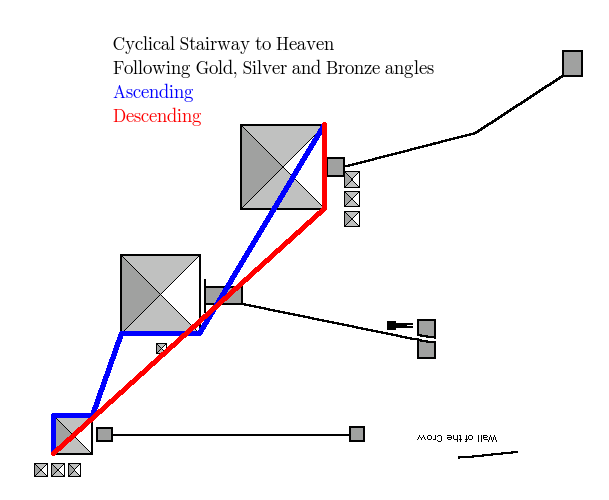
And adding in Gold…
If you can’t see the Stairway to Heaven, here is it highlighted:
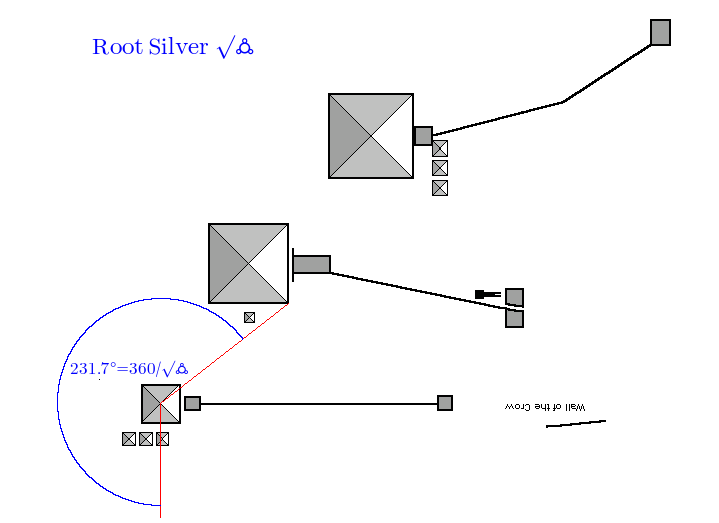
If we do the square root of the Golden Ratio, we should do the square roots of silver and bronze as well. Here’s root silver:
The angle is 231.312, we want 231.694, out by 0.382 degrees, accuracy is 99.835%
And together with silver:
Clearly an almost direct path to the heavens 🙂
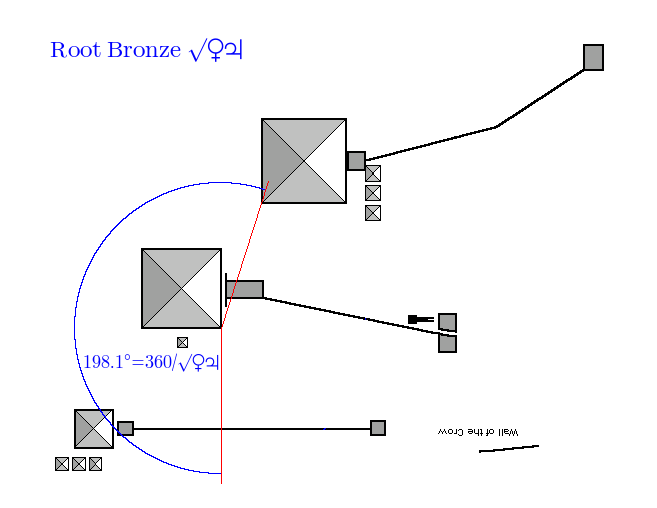
Root bronze:
The angle is 197.758, we want 198.090, out by 0.332 degrees, accuracy is 99.832 %
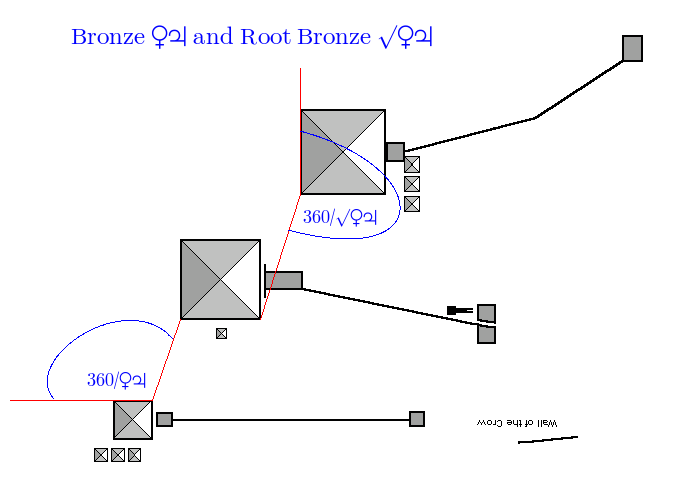
and both together:
Another quick route to the heavens 🙂
Let’s have a look at how the square roots of primes do:
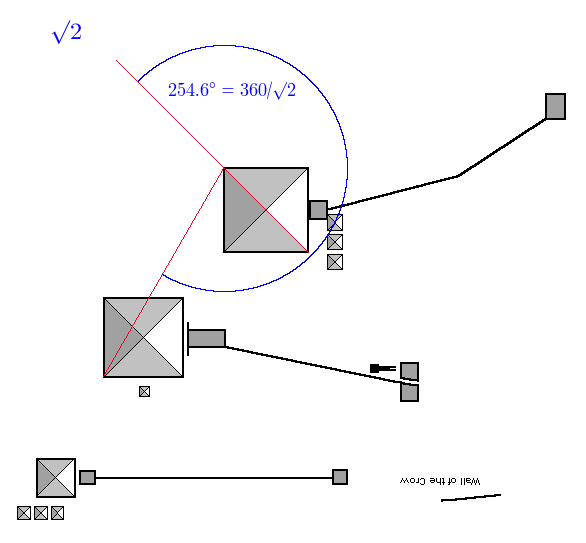
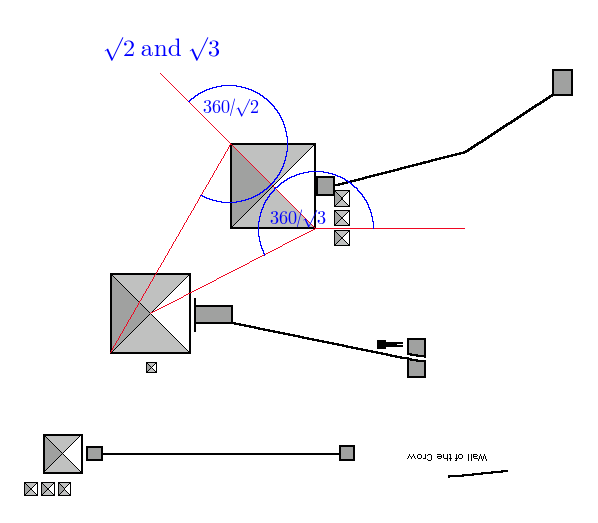
First up is root 2 (1.4142….):
The angle is 254.5154, we want 254.5584, out by 0.0430 degrees, accuracy is 99.9831%
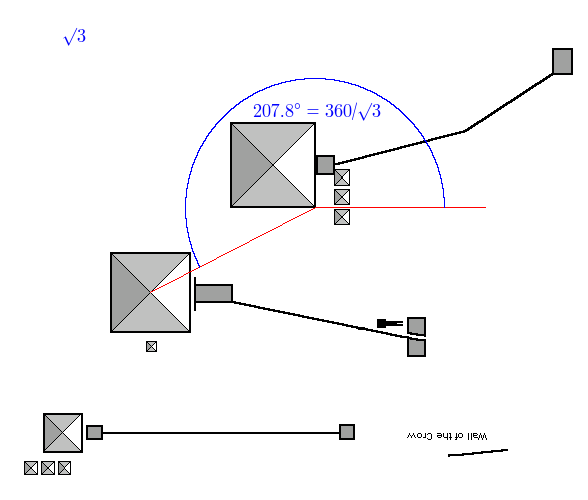
And root 3 (1.7320…):
The angle is 208.0400, we want 207.8460, out by -0.1939 degrees, accuracy is 100.0933%
For what it’s worth, the Euler–Mascheroni constant γ is 0.57721566490…. which, when multiplied by 360, gives a value of 207.7976393 which is very close to the angle above.
And both together:
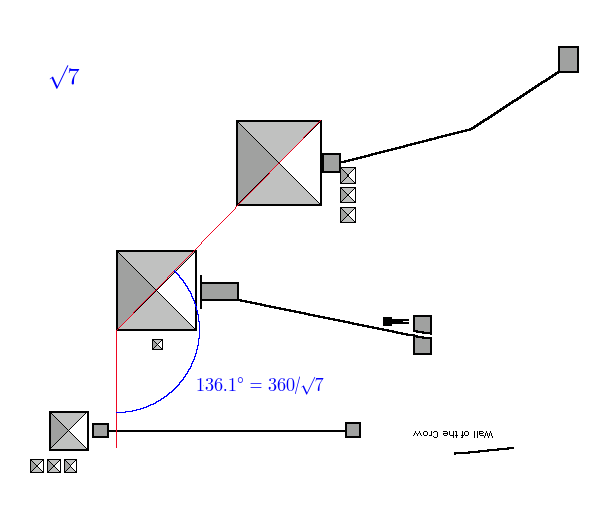
Root 7 (2.64575…) is very accurate:
The angle is 136.066, want 136.067, out by 0.0012 degrees, accuracy is 99.9992 %
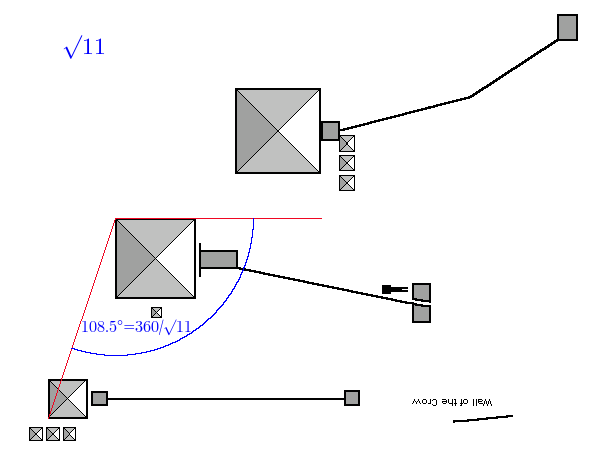
And root 11 (3.3166…)
The angle is 108.696, we want 108.544, out by -0.1519 degrees, accuracy is 100.1399%
| Name | Ratio | Point 1 | Point 2 | Calculated | Desired | AbsDiff | Percentage | Error % |
|---|---|---|---|---|---|---|---|---|
| √2 | 360/√2 | P1 TL 45° | P2 BL | 254.515 | 254.558 | 0.0430 | 99.983 | 0.017 |
| √3 | 360/√3 | P1 BR | P2 C | 208.040 | 207.846 | 0.194 | 100.093 | 0.093 |
| √7 | 360/√7 | P2 BL | P1 TR | 136.066 | 136.067 | 0.001 | 99.999 | 0.001 |
| √11 | 360/√11 | P2 TL | P3 BL | 108.696 | 108.544 | 0.152 | 100.140 | 0.140 |
There is evidence that the numbers 7 and 11 were important to the pyramid builders. For example, the height:side ratio of the great pyramid is 7:11. This may be a consequence of the building tools used, which include rods and ropes in lengths of 7 and 11 cubits.
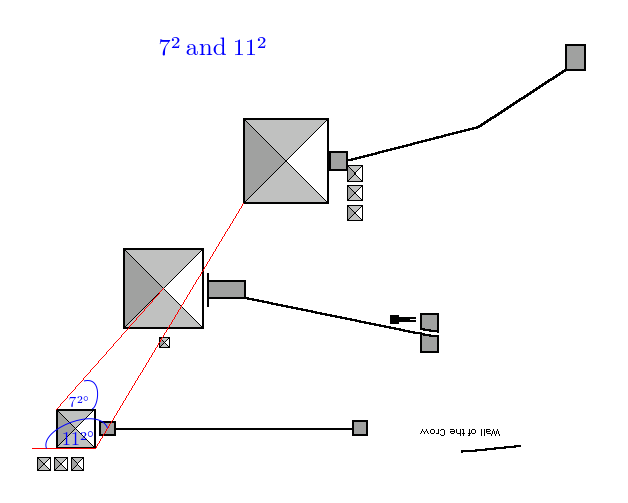
So yes, those numbers in the plan too, in the form of their roots above, and squares below:
For 11², the angle is 120.909, we want 121, out by 0.091 degrees, accuracy is 99.925%
For 7², the angle is 48.718, we want 49, out by 0.282 degrees, accuracy is 99.424 %
and 7×11:
The angle is 76.93, we want 77, out by 0.067 degrees, accuracy is 99.91%
| Name | Ratio | Point 1 | Point 2 | Calculated | Desired | AbsDiff | Percentage | Error % |
|---|---|---|---|---|---|---|---|---|
| 7x7 | 7x7 | P3 TL | P2 C | 48.718 | 49.000 | 0.282 | 99.424 | 0.576 |
| 11x11 | 11x11 | P3 BR | P1 BL | 120.909 | 121.000 | 0.091 | 99.925 | 0.075 |
| 7x11 | 7x11 | P2 C 45° | P3 C | 76.931 | 77.000 | 0.069 | 99.911 | 0.089 |
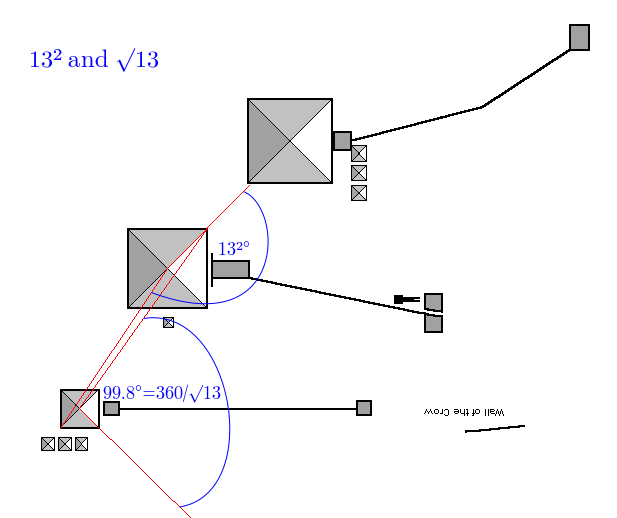
Even that famous prime number 13 puts in an appearance, in both square and root form:
For 13², the angle is 168.810, we want 169, out by 0.190 degrees, accuracy is 99.888 %
For √13, the angle is 99.670, we want 99.846, out by 0.176 degrees, accuracy is 99.824%
Here’s a summary of all the results on this page, arranged from best to worst, in terms of degree error.
| Name | Ratio | Point 1 | Point 2 | Calculated | Desired | AbsDiff |
|---|---|---|---|---|---|---|
| √7 | 360/√7 | P2 BL | P1 TR | 136.066 | 136.067 | 0.001 |
| √2 | 360/√2 | P3 C | P2 TL | 254.515 | 254.558 | 0.043 |
| 7x11 | 7x11 | P2 C 45° | P3 C | 76.931 | 77.000 | 0.069 |
| Psi | 360/ψ | P2 TR | P1 TL | 107.075 | 107.147 | 0.072 |
| φ² | 360/φ² | P3 BL | P1 BR | 137.590 | 137.508 | 0.082 |
| Phi | 360/φ | P3 BL | P1 BR | 222.410 | 222.492 | 0.082 |
| 11x11 | 11x11 | P3 BR | P1 BL | 120.909 | 121.000 | 0.091 |
| √11 | 360/√11 | P3 BL | P2 TL | 108.696 | 108.544 | 0.152 |
| √13 | 360/√13 | P3 C 45° | P2 TR | 99.670 | 99.846 | 0.176 |
| 13x13 | 13x13 | P2 C 45° | P3 BL | 168.810 | 169.000 | 0.190 |
| √3 | 360/√3 | P2 C | P1 BR | 208.040 | 207.846 | 0.194 |
| Tau | 360/τ | P3 TL | P1 TL | 57.518 | 57.296 | 0.222 |
| φ³ | 360/φ³ | P2 TR | P1 BL | 85.219 | 84.984 | 0.235 |
| 7x7 | 7x7 | P3 TL | P2 C | 48.718 | 49.000 | 0.282 |
| Root(Phi) | 360/√φ | P2 TL | P1 BR | 283.310 | 283.014 | 0.296 |
| silver | 360/(1+√2) | P1 TR | P2 BR | 149.419 | 149.117 | 0.302 |
| bronze | 360/((3+√13)/2) | P3 TR | P2 BL | 109.330 | 108.999 | 0.330 |
| root bronze | 360/sqrt((3+√13)/2) | P2 BR | P1 BL | 197.758 | 198.090 | 0.332 |
| Pi | 360/π | P2 C | P1 TL | 114.967 | 114.592 | 0.375 |
| root silver | 360/root(1+√2) | P3 BL | P2 BR | 231.312 | 231.694 | 0.382 |
| pi/phi | 360/(pi/phi) | P1 TR | P3 BL | 185.826 | 185.413 | 0.413 |
| Average | 0.206 |







Draw a line between the Khefren apex and the turning of small way to the Khufu!
It will be the 21 of June , the northern line of the morning Sun!
best wishes, Gőczey András Budapest
Giza Sun Moon
Giza timekeeper on youtube
Hi András
I find your site http://blog.world-mysteries.com/mystic-places/giza-the-time-machine/ very interesting 🙂