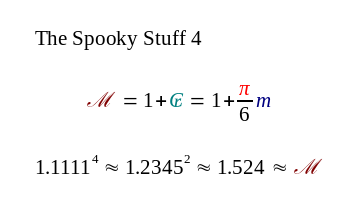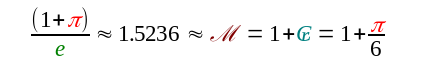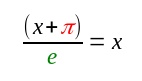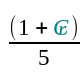To borrow a phrase from Robert Bauval, this falls under the Spooky Stuff category.
It is a very strange connection between the Grand Metre (1 + royal cubit), the base of the natural logarithm ⅇ, and the royal cubit as measured in inches.
Changelog:
2018-11-29: added Spooky Stuff 7 and 8
2018-12-03: added Spooky Stuff 9
2018-12-04: added Spooky Stuff 10
2019-04-24: added Spooky Stuff 11
Royal cubit, e and inch
I have no explanation for this. It just highlights again the ancient origins of the metre, inch and royal cubit, and how they mysteriously link together with π and ⅇ. But what about φ you ask?…. here you go:
Royal cubit, phi and yard
Questions for bonus marks:
M,e,pi
Squares and double squares
Digits 0 to 6
Grand Metre, Royal cubit, RC in inches …
Royal cubit, grand metre, pi and e
The magic of the Egyptian foot.
Seven shrieks for the nautical mile
For Spooky Stuff 10, it’s a bit more long-winded than the ones above, so need to post it in chunks.
We start with this equation as a good approximation for the Grand Metre, which is equal to 1 + the Royal Cubit:
(1 + pi )/ e
Now if we consider this equation, similar to the above:
(x + pi) / e
We can solve for x:
Solve for x
Now If we use
Foot formula
as a very close approximation for the English foot ( 0.3047197551 versus 0.3048 )
Then
Six foot formula
Which is the same as the solution for x above, to 4 decimal places.
So,
(1 + pi) / e
gives us the Grand Metre which is 5 English feet, while the solution to
(x + pi_ / e
gives us 6 English feet.
Spooky Stuff 11
We have already seen on other pages about the cubit, how the natural logarithm base e pops up in approximations of the royal cubit, for example {\varphi e} \over 8.4 or {{1 + \pi} \over {e}} -1 = ₢
There’s even a formula to approximate the inch, as follows: {\pi e} \over 336
Then yesterday Youtube delivered up two interesting videos:
and one of the videos in this series, can’t find the exact one now:
Anyway they point out an interesting correlation between e and the imperial foot, which goes like this:
e – 1 = 2.71828 – 1 = 1.71828
1 inch = 25.4mm, so 1 foot = 12 x 25.4 = 30.48 mm.
Convert to metres, gives 0.3048 m
The royal cubit ₢ = π/6 = 0.5236 m
Divide the cubit by the foot …. 0.5236 / 0.3048 = 1.7178 (all calculations rounded to 4 decimals so far)
If we subtract actual answer above from (e – 1), we get 0.000438 … which is a fraction of a millimetre difference ( less than 500 microns which is less than the length of a grain of sand, salt or sugar) between (e -1) and ₢/foot.
Which neatly links ₢, e and the foot…. and from the foot back to the inch.