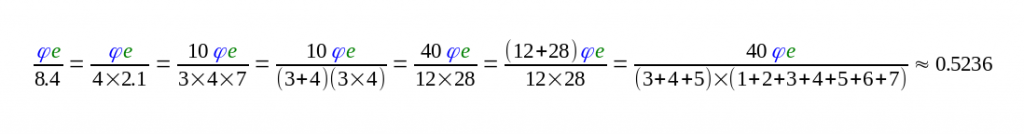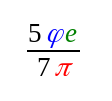[Note: for older version and discussion, see No body parts were harmed producing this post. ]
[Note 2: for newer version, see 5 Different methods of getting the 10 parts of a cubit. ]
[Changelog:
2018-11-26: My gut had been insisting for a long time that there was another formula involving pi, phi and e involved with these cubit parts, and eventually today I found it. Not only is it incredibly simple (in basic form) but also incredibly accurate. The basic form is simply (phi x e)/pi = φe/π, which comes out at 1.400013584. If we divide this by 7, we get 0.2000 m, and from that can scale to 0.3000 m, and from that, to the other subdivisions. Have updated the formulas in the PDF attached. I’m particularly chuffed with the formula for the foot…. 🙂
2018-11-30: Added formulas based on √(π²+φ²)/e
2018-12-02: Added formulas for great span and remen based on φπ/e construction.]
While playing around with my calculator in recent times, manipulating pi, phi, e, and the cubit e.t.c., I sometimes ended up with an answer of 1.199981615 which is extremely close to 1.2, and I thought that was interesting. Eventually I took note of the formula to get there, and then realised that 1.2 m is 4 Egyptian feet … and then the penny dropped.
From the foot, we can double to the pole, or half to the double handbreadth. A bit of playing around revealed reasonably easy adjustments to give other fractions of the cubit, all based off the same ratio, which is simply pi over (phi squared) = π/φ².
So here’s an updated list of cubit parts, plus some other measurements like assorted feet, in PDF form. Posting screengrabs from LibreOffice Math is getting tedious 🙂
cubit-parts.pdf